Landmeten op het schoolplein

In dit artikel nemen wij u mee naar het land van Berend Botje. Op verrassende wijze krijgt u een nieuwe kijk op de topografie van Nederland. Het enige dat u nodig hebt, is wat fantasie. Na afloop van het verhaal vindt u nog enkele praktische handreikingen om aan de slag te kunnen in de klas.

Waarom landmeten?

Niet inperken, maar uitbreiden

We willen omgaan met verschillen. Ook bij de ruimtelijke oriëntatie. Dit artikel is bedoeld voor leerkrachten, die iets nieuws willen uitproberen. Om in het kort te verhelderen waarom we dit artikel geschreven hebben, verwijzen we naar het boekje Ongewild Lastig (Huizen, 2005). Hierin wijzen de auteurs op de andere leerstijl van kinderen met bijvoorbeeld ADHD. Ook komt hun behoefte aan concreet materiaal en levensechte leersituaties aan bod.
Dit artikel speelt op die behoefte in. Het artikel is bruikbaar naast elke methode vanaf groep 6 en geeft antwoord op de vraag: hoe kan een bovengemiddeld begaafd kind samenwerken met een kind dat gehinderd wordt door een ordeningsprobleem en frustratie over tegenvallende topografieresultaten?
U staat mogelijk op het punt om de stof voor het laatstgenoemde kind in te perken. Want de aanpak van ADHD is vaak gericht op inperken van gedrag en/of leerstof. Wij stellen u echter voor om juist uit te breiden en om gebruik te maken van de diverse talenten van de leerlingen.
Nodig de kinderen uit om te kijken, te voelen, te ervaren en te doen in de klas of buiten op het schoolplein. Het ruimtelijk-wiskundige en het werkelijkheidsnabije zijn in de beschreven aanpak verweven. Topografie heeft immers van oudsher iets met landmeten. En veel kinderen hebben iets met floorgames.
Nota bene. Zie in dit verband het artikel Het Wereldspel, dat is opgenomen in Praxisbulletin, 26ste jaargang, nummer 3, november 2008.

Landmarks inmeten

Als het om topografie gaat, kan niets de voetreis naar Rome vervangen. Een goed alternatief is om bij de kinderen te informeren wat zij als landmarks ervaren. (En dat kan oma’s huis in Deventer zijn, maar ook IKEA-Utrecht of het pannenkoekenhuis Meyendel.) Laat de kinderen die landmarks inmeten, binnen de structuur die dit artikel biedt. Topografie komt hiermee los uit de atlas en ook los van het beeldscherm. Geef uw leerlingen de vrijheid om hun landmarks een ingeschatte plek te geven. We willen landmeten combineren met de durf van de zondagsschilder. Vóór alles gaan we dit laatste waarderen, zodat er veiligheid ontstaat, waarin ook wiskundige inzichten kunnen opbloeien.
Het zal nu nog raadselachtig klinken, maar kinderen hebben met een meetlint in de hand snel door dat de afstand van Drachten naar de monding van de Elbe een referentiemaat is voor de juiste verlenging in tegenovergestelde richting naar het Haringvliet.
Nota bene. De internetuitbreiding bij dit artikel kan dit verhelderen. Echter… beschouw het Haringvliet – ter hoogte van IJmuiden – vooral als een kans voor een leuke nabespreking. Want preciezer landmeten komt vanzelf!

Kaarsrechte grenzen

Canadese wijsheid

Heeft Canada een koning, een keizer of een admiraal? In alle gevallen is het iemand, die nooit land verovert. De grenzen van Canada zijn immers kaarsrecht. En dat wijst op wijsheid. De Canadezen blazen namelijk elke veldtocht halverwege af. Die gewoonte heeft kracht van wet. Zo kunnen de soldaten even flink marcheren. Iedereen is moe en voldaan. Vergelijk het met de hond uitlaten. De strijdrossen hebben gepoept en van andere grassen gesnoept. Ze hebben geen kanon horen dreunen en tóch mogen ze al terug naar de stal.
Leg uw liniaal maar eens langs de grens tussen Canada en Alaska. Kaarsrechte topografie! Nergens een spoor te vinden van een grensconflict!

Berend Botje

Met deze Canadese wijsheid in het achterhoofd nemen wij u mee naar het land van Berend Botje. We maken een sprong naar Zuidlaren. Nadat Berend Botje zijn bootje heeft achtergelaten, wil hij met zijn leger via Drenthe naar Groningen marcheren. Over een half in het moeras verzonken knuppelpad, door stugge heide en rul zand, tot hij plotseling genoeg krijgt van die veldtocht, want… de weg was recht en dan weer krom. Hij blaast de hele oorlog daarom op Canadese wijze af. Nooit kwam Berend Botje weerom…
Hij arriveert in Leeuwarden, laat zijn strijdrossen op stal zetten en organiseert een conferentie voor de Wereldtop. Ook koningen, keizers en admiraals verzamelen zich om de ronde Friese conferentietafel. Professoren, prinsessen, notabelen, sultans en landmeters, ze zijn allen in naam van vredige grenzen te gast in Leeuwarden.
We kunnen die gasten hier niet allemaal bij naam noemen. Voor de hertogin van Canada en de grootvizier van Alaska maken we een uitzondering. Zij geven een presentatie, met als titel: Peaceful borders of Canada and Alaska. Zij maken iedereen enthousiast voor kaarsrechte topografie.
Nota bene. Het verhaal mag in een later stadium gerelativeerd worden. Kaarsrechte grenzen zijn niet altijd peaceful tot stand gekomen. (Zie de internetuitbreiding bij dit artikel.)

Drachten als middelpunt

Kaarsrecht? Moet Friesland dan een vierkant worden? De volle, bolle Friese koning roept uit: “Nee! Friesland zal een cirkel worden!”
Hij heft zijn glas en steekt zijn vork met kracht in het middelpunt van de ronde tafel. Hij bast: “Drachten is het middelpunt! Punt, uit! Proost!”
Velen heffen het glas met hem, zo niet de fijnbesnaarden. De rector magnificus van Groningen stoot zijn glas om van schrik. Iedereen weet toch dat Grouw in het Friese midden ligt! Als je Drachten als middelpunt neemt, dan leidt dit tot provinciale landroof!
De Groningse rector wil echter niet brutaal doen tegen de Friese koning. Hij draait eromheen, met een verhaal over de oeroude rechten van het Groningse Westerkwartier. Ook hij is natúúrlijk een groot voorstander van wiskundig bepaalde grenzen. Maar Friesland – het hoge woord floept er toch uit – kan géén cirkel worden! Er moet een kwart uit die Friese cirkel, om ruimte te maken voor het Groningse kwart. In Groningen noemen ze dat het Westerkwartier.

Een vierkant in de Friese cirkel

De Friese koning voelt dat het gesprek de verkeerde kant op gaat en staat dreigend op. Hij kijkt om zich heen of hij ergens mee kan smijten… Die kandelaar daar! De hertogin van Canada schudt echter kalm haar hoofd en de Fries laat zijn arm halverwege zakken voor zo veel gezag. De hertogin slaat een arm om zijn brede schouders en fluistert iets in zijn oor. Als bij toverslag ontspannen zijn kaken zich.
De rector magnificus put daar moed uit en tekent met onzekere hand een vierkant in de Friese cirkel. Bij de hoekpunten van het vierkant komen Drachten, Lauwersoog, Roodeschool en de stad Groningen.
Hij maakt een in Lauwersoog beginnende diagonaal dubbel zo lang tot Ter Apel. En ook de zuidelijke zijde van het vierkant maakt hij twee keer zo lang: van Drachten via Groningen tot Nieuweschans. Groningen is een vierkant plus een parallellogram. (Zie figuur 1.)

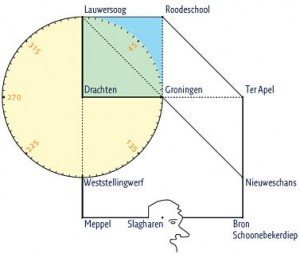
Figuur 1: de Friese cirkel en het Groningse vierkant.

Per acclamatie besloten!

Berend Botje kijkt welwillend naar de nieuwe grenzen. Hij slaat met zijn voorzittershamer en roept: “Aldus besloten!”
Berend Botje heeft haast, want hij wil als voorzitter van de conferentie nog iets extra’s uit het vuur slepen. Het blijkt, dat hij een monument voor zichzelf wil oprichten, door Drenthe de vorm van zijn eigen hoofddeksel te geven. Hij meesmuilt dat zijn afgeblazen veldtocht immers al helemaal tot aan Zuidlaren reikte.
Per acclamatie besloten! Drenthe krijgt de vorm van Berend Botjes kapiteinssteek! De lijn Weststellingwerf-Meppel ligt precies in het verlengde van de lijn Lauwersoog-Drachten en is precies de helft daarvan in lengte. De lijn van Ter Apel naar de bron van het Schoonebekerdiep heeft dezelfde lengte. Met één pennenstreek worden de bochten van het Schoonebekerdiep rechtgetrokken.
Tot op de dag van vandaag loopt de zuidelijke grens daar bij Ponypark Slagharen om een vorm heen, die op het hoofd van Berend Botje lijkt!

Kom mee naar buiten!

Landmeten met de kompascirkel

Tot zover Berend Botje. Het hele verhaal dient als denkmodel, waarmee kinderen in de midden- en bovenbouw de West-Europese kust – met de trechtermondingen van de Seine tot de Elbe – kunnen tekenen. Op elke gewenste schaal! Op de schaal van een A4’tje tot die van het schoolplein.
De kinderen beginnen altijd met de Friese cirkel. Op papier kan die getekend worden met een passer of een schoteltje. Maar op het schoolplein is een landmeetapparaat nodig. Te weten: een stevige kompascirkel, met aan het middelpunt een touw, met daaraan een stuk stoepkrijt. (Zie figuur 2.) Aan de noordpijl is een kompas gelijmd, zodat de straal van Drachten naar Lauwersoog inderdaad op het noorden gepositioneerd kan worden: Nederland zoals het in werkelijkheid ligt.

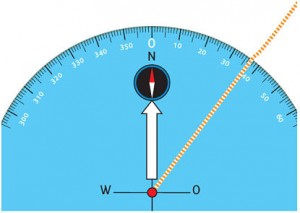
Figuur 2: kompascirkel.

Nota bene. U kunt een werktekening van de kompascirkel downloaden via internetuitbreiding bij dit artikel. Lijm de cirkel samen met een kompasje op een stuk karton (of een plankje). Vanuit het midden kan een touwtje – met daaraan een stuk stoepkrijt – gespannen worden voor het maken van de Friese cirkel.

West-Europese trechtermondingen

De West-Europese trechtermondingen liggen op een lijn, die de Friese cirkel en het Groningse vierkant in tweeën snijdt. Precies op de oost-westdiagonaal (Roodeschool-Drachten) van het Groningse vierkant.
In figuur 3 is de monding van de Eems ingekleurd. De afstand van Drachten tot en met de Eems is dezelfde als de afstand van de Eems tot de Weser en ook van de Weser tot en met de Elbe.

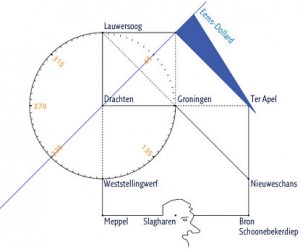
Figuur 3: monding van de Eems.

Voor het gemak tekenen we alle trechtermondingen – van de Seine tot en met de Elbe – als driehoeken, die tegen een lijn aan liggen.
De reuzensprong vanuit Drachten over de Elbe heen is de maat voor de afstand van Drachten tot en met het Haringvliet. Dan volgen op kleine afstand van elkaar: de Grevelingen, de Oosterschelde en de Westerschelde. Daarna volgt dezelfde reuzensprong als hierboven naar de monding van de Somme in Frankrijk. En de laatste reuzensprong gaat naar de monding van de Seine.
U ziet dat de Nieuwe Waterweg een andere schematische vorm heeft dan de rest. De Nieuwe Waterweg is weergegeven als een rechthoek en alle andere trechtermondingen hebben de vorm van een driehoek. (Zie figuur 4.) Dit komt omdat door kanalisatie en door de aanleg van pieren in de zee de Nieuwe Waterweg geen trechtermonding meer is.
Nota bene. Het Haringvliet, de Grevelingen en de Oosterschelde kunnen natuurlijk ook geen échte trechtermondingen meer worden genoemd, maar laten we die de driehoeksvorm nog maar even gunnen.

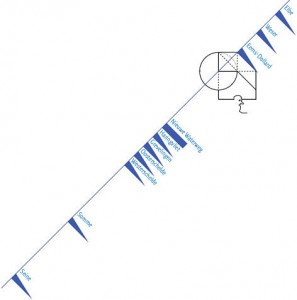
Figuur 4: reuzensprongen van Seine tot Elbe.

Ruggenwervel

Nu kunnen de rivieren nog getekend worden. Het is leerzaam eerst te tekenen met fantasie en later pas naar de werkelijkheid te kijken. Laat maar kronkelen, die blauwe lijnen! En wat te denken van écht water? Met een gietertje kunnen grillige rivieren gemaakt worden op de stoeptegels.
De tekening van de trechtermondingen is de ruggenwervel voor allerlei schetsen van Nederland en België. (Zie figuur 5.) Vanuit Weststellingwerf kan bijvoorbeeld een cirkel gemaakt worden, waarbinnen de Waddeneilanden plus Den Helder gedacht kunnen worden. En de kustlijn naar Hoek van Holland is dan ook te schetsen.

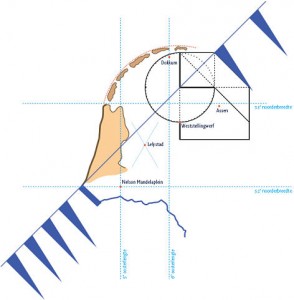
Figuur 5: ruggenwervel voor schetsen van Nederland en België.

Didactische beer

Waar staat uw school ergens, gezien vanuit Drachten? Laat de kinderen een touw vanuit Drachten straktrekken over de geschatte schoollocatie en met behulp van het landmeetapparaat het getal van de kompasstreek bepalen.
Als ze dit een keertje gedaan hebben, dan kan de kompascirkel op de geschatte schoollocatie worden geplaatst en dan is de didactische beer los…
Welke kant moet je op als je op vakantie naar Marokko gaat? Geef de kinderen een kleine kompascirkel om ermee over landkaarten te schuiven. En geef ze die grotere, met het kompas, het stoepkrijt en het touw, om buiten op het schoolplein te tekenen wat ze in de atlas ontdekken.

Tot slot

Bent u enthousiast geraakt en wilt u aan de slag in de klas? Dan kunt u op de website van het Praxisbulletin meerdere voorbeelden en toepassingen vinden. Zo is de cirkel bijvoorbeeld ook heel geschikt voor het oefenen van tafels, delingen en breuken. Tevens kunt u op de website een meer uitgebreide versie van de kompascirkel vinden, in de vorm van een landmeetapparaat.

Veel succes!