Over het taalprobleem in het rekenonderwijs. Taalgericht rekenen, als steun bij het begrijpen van contextgebonden sommen. Over taalproductie, taalsteun en taalfeedback.
“Wat is uw convictie nopens de syndicaat van lingua franca annex calculatie?”
Het is best lastig, om antwoord te geven op een vraag, als je niet begrijpt wat er gevraagd wordt. Dit probleem komt helaas ook bij veel kinderen voor. Kinderen, die moeite hebben met taal, merken, dat dit ook moeilijkheden geeft tijdens andere vakken, zoals rekenen. Van de kinderen, die moeite hebben met de Nederlandse taal, is een grote groep allochtoon. Maar ook autochtone kinderen hebben soms een taalachterstand. De context, die er juist voor hoort te zorgen, dat kinderen de sommen beter begrijpen en kunnen plaatsen, wordt op deze manier geen hulpmiddel, maar juist een obstakel! Het is natuurlijk doodzonde, als kinderen niet mee kunnen komen met de rekenlessen, niet omdat ze het niet kúnnen, maar omdat ze niet begrijpen wat er van hen gevraagd wordt! Wat kunnen we doen, om kinderen te helpen met de contextsommen, die in de huidige rekenmethoden veelvuldig te vinden zijn? Daarover gaat dit artikel.
Een probleem, twee oplossingen
Traditioneel rekenen
Er zijn verschillende mogelijkheden om een eventueel taalprobleem in het rekenonderwijs te benaderen. Voorstanders van traditioneel rekenen kwamen met de suggestie, om alle taal uit de rekenmethoden te halen. (Schöttelndreier, Wiskunde-aversie verdeelt experts, 1999.) Teksten zouden volgens hen alleen maar afleiden van waar het in deze methoden werkelijk om draait: het rekenen. Een “kaal” rekenboek, met alleen maar cijfers en sommen, zou volgens de voorstanders van traditioneel rekenen uitkomst bieden.
Taalgericht rekenen
Een belangrijk aspect van het rekenen is, dat het toegepast moet kunnen worden in de praktijk. Een andere oplossing voor het probleem is dan ook: taalgericht rekenen. Taalgericht rekenen biedt steun bij het begrijpen van contextgebonden sommen, zodat leerlingen ook buiten hun rekenboek in staat zijn hun wiskundige kennis toe te passen. (Streun, Samenhang als recept voor goed rekenonderwijs, 2010.) De leerlingen worden geholpen de taal in hun rekenboek te begrijpen en ontwikkelen zich zo op zowel taal- als rekengebied.
Pijlers taalgericht rekenonderwijs
Om goede, taalgerichte rekenlessen te kunnen geven, moeten er drie pijlers in de lessen verwerkt worden, namelijk: taalproductie, taalsteun en taalfeedback.
TAALPRODUCTIE
Taalproductie is de tijd, dat leerlingen zélf aan het woord zijn. Bijvoorbeeld: bij het beantwoorden van een vraag of het werken in groepjes. In dit verband kan er zowel sprake zijn van horizontale communicatie, als van verticale communicatie. Horizontale communicatie is de communicatie tussen twee of meer leerlingen. Verticale communicatie is de communicatie tussen een leerkracht en een leerling. (Vos & Schoenmaker, Geïntegreerde communicatie, 2007.)
TAALSTEUN
Taalsteun houdt in, dat een leerkracht signaleert wat leerlingen nog moeilijk vinden qua taal en hier ondersteuning geeft waar nodig. Ook betekent dit, dat de leerkracht begrijpelijke taal spreekt. Vooral ook omdat er onderscheid kan worden gemaakt tussen schooltaal en de taal die leerlingen thuis gebruiken. CAT is Cognitieve Academische Taal (schooltaal) en DAT is de Dagelijkse Algemene Taal (thuistaal). (Appel, 1984, in: Van Eerde, Rekenen-wiskunde en taal: een didactisch duo, 2009.)
Een leerkracht moet er in zijn/haar lessen rekening mee houden, dat de schooltaal en de thuistaal van een leerling kunnen verschillen. Daarom is het belangrijk leerlingen te laten vertellen wat ze al weten over bijvoorbeeld het rekenprobleem. De leerkracht kan dan signaleren of leerlingen wel of niet moeite hebben met de schooltaal. Als leerlingen de schooltaal niet kennen, kan dat het rekenen in de weg zitten.
TAALFEEDBACK
Taalfeedback is het geven van feedback op de taaluitingen van leerlingen. Het is overigens belangrijk om dat niet te nadrukkelijk te doen. Een leerling kan bijvoorbeeld zeggen: “Ik loopte gisteren op de markt.” Een leerkracht zou dan natuurlijk kunnen zeggen: “Het is liep. Ik liep op de markt.” Maar dat kan bij de leerling voor een ongemakkelijk gevoel zorgen. Beter is het om een antwoord te geven in de trant van: “O, liep jij gisteren op de markt?” Dan hoort de leerling namelijk óók wat de goede vorm van het woord is, maar zónder dat hij/zij door de leerkracht nadrukkelijk wordt verbeterd. En dit zorgt ervoor, dat de leerling in het vervolg ook nog gewoon in de klas durft te spreken, zonder de angst te hebben, dat de hele klas hoort dat hij/zij verbeterd wordt. Dit houdt het pedagogisch klimaat in de klas goed en veilig.
Contextuele inbedding
INZICHT
Het is belangrijk, om nieuwe stof aan te bieden in een betekenisvolle context. Dit wordt ook wel contextuele inbedding genoemd (Gravemeijer, 2002). Dit kan gebeuren door gebruik te maken van afbeeldingen of van onderwerpen, die de kinderen aanspreken.
Een voorbeeld hiervan is: het aanleren van breuken, aan de hand van een taart. Door te beginnen met het tekenen van taarten en het praten over eerlijk verdelen, krijgen de leerlingen inzicht in het abstracte begrip van breuken.
VERDUIDELIJKEN, NIET AFLEIDEN!
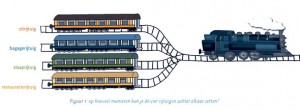
Als een methode contextuele inbedding van een rekenkundig probleem voorschrijft (of als u daar als leerkracht zelf voor kiest), dan is het belangrijk, dat die context voor verduidelijking zorgt. Want er zijn helaas ook heel veel contexten, die alleen maar voor afleiding en/of verwarring zorgen bij de leerling. Een goed voorbeeld hiervan zijn de verschillende interpretatiemogelijkheden van een afbeelding.
ANTWOORDEN
Als leerlingen de vraag onder de afbeelding lezen en vervolgens het plaatje bekijken, dan zouden de volgende antwoorden gegeven kunnen worden:
1 “De rijtuigen passen op geen enkele manier achter elkaar, want het spoor is te kort om alle rijtuigen neer te zetten.”
2 “Nou, het restauratierijtuig wordt gerestaureerd, dus die rijdt al niet mee. Dan blijven er maar twee manieren over.”
3 “Toen ik met de trein ging, reed het restauratierijtuig helemaal vooraan, daarachter kwam het slaaprijtuig en daarachter het bagagerijtuig. Dus het kan maar op één manier.”
4 “Als ik met de trein reis, dan zijn er deze gekke rijtuigen niet, alleen maar zitplaatsen voor mensen.”
Vraag en afbeelding leiden in dit geval tot verwarring. In ieder geval niet tot eenduidigheid en duidelijkheid voor de leerlingen, waardoor ze het rekenkundig probleem kunnen oplossen.
Hoe maak je een taalgerichte rekenles?
TWEE MANIEREN
Er zijn twee manieren om een taalgerichte rekenles te ontwerpen:
– De eerste manier is, om een bestaande rekenles om te bouwen tot een taalgerichte rekenles, zodat er meer aandacht voor taal in de les wordt verwerkt.
– De tweede manier is, om zélf een rekenles te bedenken en hier taaldoelen aan te koppelen.
BEDENKEN
Wij hebben lessen ontworpen rondom de rekenthema’s breuken, procenten, verhoudingen en kommagetallen. Ieder ander onderwerp is natuurlijk ook mogelijk.
Werkwijze
– De eerste stap is het kiezen van een onderwerp.
– De tweede stap is om de rekendoelen helder te krijgen.
– Hierna kunt u gaan bekijken welke taaldoelen het best bij deze rekenles passen.
– Vervolgens kiest u een werkvorm, die past bij de les, de doelen en uw klas.
Het is belangrijk, dat u ervoor zorgt, dat de taal- en rekendoelen in gelijke mate aan de orde komen. De rekendoelen zijn dus niet superieur aan de taaldoelen!
OMBOUWEN
Om taalgerichte rekenlessen te geven, hoeft u ze overigens niet iedere keer zelf te bedenken. Er is niets mis mee om een bestaande methodeles om te bouwen.
Aandachtspunten
– Als u zo’n bestaande rekenles ombouwt naar een taalgerichte rekenles, dan zijn de rekendoelen en het onderwerp al helder.
– Kijk dan voor de taaldoelen eens door de ogen van een kind uit uw klas. Welke woorden zouden de kinderen moeilijk kunnen vinden? Door zo’n woord te bespreken of uit te leggen, kunt u veel kinderen op weg helpen bij het begrijpen van de rekenles.
– Schenk ook aandacht aan de afbeelding. Wat wordt hier nu precies mee bedoeld? Is de afbeelding functioneel voor de opgave? Of heeft de afbeelding nog wat extra uitleg nodig?
In de praktijk
POSITIEVE EFFECTEN
Onze eigen ervaringen met taalgerichte rekenlessen zijn overwegend positief. Zo zorgen deze lessen voor afwisseling. Het is namelijk noodzakelijk om te overleggen, om tot de betekenis van de zogenoemde CAT (Cognitieve Academische Taal; schooltaal) te komen. Kinderen worden hier enthousiast van en leren ook meer door te overleggen (Bongaards & Sas, 2009). Het mes van taalgericht rekenonderwijs snijdt aan twee kanten. De rekenresultaten worden beter, omdat de contextsommen beter begrepen worden, dankzij de contextuele inbedding en de drie pijlers van taalgericht rekenonderwijs. Tegelijkertijd worden de taalresultaten ook beter, omdat er veel meer tijd aan taal wordt besteed naast de reguliere taallessen.
PROCESGERICHT
Uit de praktijk blijkt, dat veel leerkrachten al onbewust aan verschillende aspecten van taalgericht rekenonderwijs werken, door bijvoorbeeld standaard de context en de woorden die daarbij horen uit te leggen. Dit is een positief uitgangspunt, dat nog verder verbeterd zou kunnen worden, mits er bewust mee wordt omgegaan. Dat wil zeggen, dat de leerkracht vragen stelt om complexe, cognitieve taalfuncties te stimuleren. Een van deze functies is bijvoorbeeld het onder woorden brengen van gedachten, iets waar veel leerlingen moeite mee hebben. Bij taalgerichte rekenlessen ligt de nadruk dus ook op het proces en niet op het product!
ONDERSTEUNING
In taalgerichte rekenlessen worden meer doelen behaald dan bij de rekenlessen, die in de rekenmethode beschreven staan. Wél wordt er bij de meeste taalgerichte rekenlessen aan dezelfde taalleerlijnen gewerkt, namelijk: woordenschat en mondelinge communicatie. Daarom is het belangrijk om te noemen, dat de taalgerichte rekenlessen de reguliere taallessen niet overnemen, maar juist ondersteunen. Door tijdens rekenen al aan deze taalleerlijnen te werken, blijft er meer tijd over voor de overige taalontwikkeling in de reguliere taallessen.
MOGELIJKHEDEN
Het mag inmiddels duidelijk zijn, dat de taalkundige kant van het rekenonderwijs op verschillende manieren gebruikt, geïnterpreteerd en toegepast kan worden. Het belangrijkste doel waarnaar gestreefd moet worden, is een juiste invulling van de context van de som. Deze context moet niet alleen toepasbaar en logisch zijn, maar vooral ook begrijpelijk en eenduidig.
Wellicht is er niet één juiste methode, die als norm toegepast zou kunnen worden. Daarvoor zijn de eventuele moeilijkheden, waar kinderen en leerkrachten in het onderwijs tegenaan kunnen lopen misschien wel te divers. Maar dat er mogelijkheden zijn om het huidige rekenonderwijs, in ieder geval op taalkundig gebied, aan te vullen en efficiënter toe te passen, is een ding dat zeker is.
Tot slot
Misschien vraagt u zich nog steeds af welke vraag wij u stelden aan het begin van dit artikel. We vroegen u wat uw mening is over de combinatie van taal en rekenen. Wellicht kunt u daar nu – na het lezen van dit artikel – een antwoord op geven.
Veel succes!